J.J. del Pozo, P.L. Garrido, P.I. Hurtado
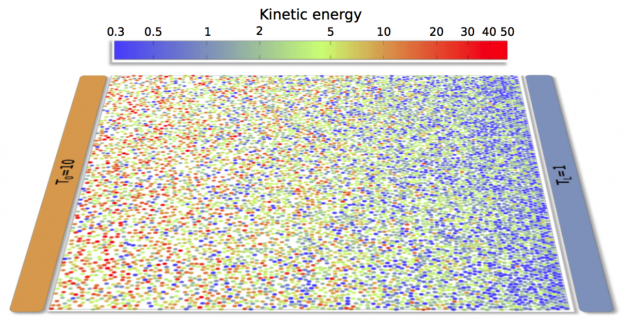
When driven out of equilibrium by a temperature gradient, fluids respond by developing a nontrivial, inhomogeneous structure according to the governing macroscopic laws. Here we show that such structure obeys strikingly simple scaling laws arbitrarily far from equilibrium, provided that both macroscopic local equilibrium and Fourier’s law hold. Extensive simulations of hard disk fluids confirm the scaling laws even under strong temperature gradients, implying that Fourier’s law remains valid in this highly nonlinear regime, with putative corrections absorbed into a nonlinear conductivity functional. In addition, our results show that the scaling laws are robust in the presence of strong finite-size effects, hinting at a subtle bulk-boundary decoupling mechanism which enforces the macroscopic laws on the bulk of the finite-sized fluid. This allows to measure for the first time the marginal anomaly of the heat conductivity predicted for hard disks.
Additional material: video demonstrating the scaling procedure (credit: J. del Pozo 2014)
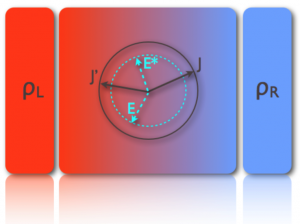Understanding the physics of nonequilibrium systems remains as one of the major challenges of theoretical physics. This problem can be cracked in part by investigating the macroscopic fluctuations of the currents characterizing nonequilibrium behavior, their statistics and associated structures. This fundamental line of research has been severely hampered by the overwhelming complexity of this problem. However, during the last years two new general methods have appeared to investigate fluctuating behavior that are changing radically our understanding of nonequilibrium physics: a powerful macroscopic fluctuation theory (MFT) and a set of advanced computational techniques to measure rare events. In this work we study the statistics of current fluctuations in nonequilibrium diffusive systems, using macroscopic fluctuation theory as theoretical framework, and advanced Monte Carlo simulations of several stochastic lattice gases as a laboratory to test the emerging picture. Our quest will bring us from (1) the confirmation of an additivity conjecture in one and two dimensions, which considerably simplifies the MFT complex variational problem to compute the thermodynamics of currents, to (2) the discovery of novel isometric fluctuation relations, which opens an unexplored route toward a deeper understanding of nonequilibrium physics by bringing symmetry principles to the realm of fluctuations, and to (3) the observation of coherent structures in fluctuations, which appear via dynamic phase transitions involving a spontaneous symmetry breaking event at the fluctuating level. The clear-cut observation, measurement and characterization of these unexpected phenomena, well described by MFT, strongly support this theoretical scheme as the natural theory to understand the thermodynamics of currents in nonequilibrium diffusive media, opening new avenues of research in nonequilibrium physics.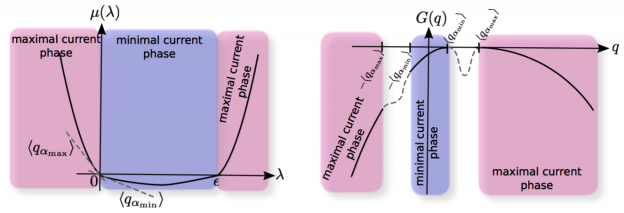
We consider fluctuations of the dissipated energy in nonlinear driven diffusive systems subject to bulk dissipation and boundary driving. With this aim, we extend the recently-introduced macroscopic fluctuation theory to nonlinear driven dissipative media, starting from the fluctuating hydrodynamic equations describing the system mesoscopic evolution. Interestingly, the action associated to a path in mesoscopic phase-space, from which large-deviation functions for macroscopic observables can be derived, has the same simple form as in non-dissipative systems. This is a consequence of the quasi-elasticity of microscopic dynamics, required in order to have a nontrivial competition between diffusion and dissipation at the mesoscale. Euler-Lagrange equations for the optimal density and current fields that sustain an arbitrary dissipation fluctuation are also derived. A perturbative solution thereof shows that the probability distribution of small fluctuations is always gaussian, as expected from the central limit theorem. On the other hand, strong separation from the gaussian behavior is observed for large fluctuations, with a distribution which shows no negative branch, thus violating the Gallavotti-Cohen fluctuation theorem as expected from the irreversibility of the dynamics. The dissipation large-deviation function exhibits simple and general scaling forms for weakly and strongly dissipative systems, with large fluctuations favored in the former case but heavily supressed in the latter. We apply our results to a general class of diffusive lattice models for which dissipation, nonlinear diffusion and driving are the key ingredients. The theoretical predictions are compared to extensive numerical simulations of the microscopic models, and excellent agreement is found. Interestingly, the large-deviation function is in some cases non-convex beyond some dissipation. These results show that a suitable generalization of macroscopic fluctuation theory is capable of describing in detail the fluctuating behavior of nonlinear driven dissipative media.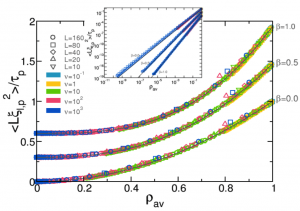
We consider a general class of nonlinear diffusive models with bulk dissipation and boundary driving, and derive its hydrodynamic description in the large size limit. Both the average macroscopic behavior and the fluctuating properties of the hydrodynamic fields are obtained from the microscopic dynamics. This analysis yields a fluctuating balance equation for the local energy density at the mesoscopic level, characterized by two terms: (i) a diffusive term, with a current that fluctuates around its average behavior given by nonlinear Fourier’s law, and (ii) a dissipation term which is a general function of the local energy density. The quasi-elasticity of microscopic dynamics, required in order to have a nontrivial competition between diffusion and dissipation in the macroscopic limit, implies a noiseless dissipation term in the balance equation, so dissipation fluctuations are enslaved to those of the density field. The microscopic complexity is thus condensed in just three transport coefficients, the diffusivity, the mobility and a new dissipation coefficient, which are explicitly calculated within a local equilibrium approximation. Interestingly, the diffusivity and mobility coefficients obey an Einstein relation despite the fully nonequilibrium character of the problem. The general theory here presented is applied to a particular albeit broad family of systems, the simplest nonlinear dissipative variant of the so-called KMP model for heat transport. The theoretical predictions are compared to extensive numerical simulations, and an excellent agreement is found.
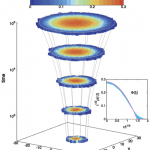We analyze the spread of a localized peak of energy into vacuum for nonlinear diffusive processes. In contrast with standard diffusion, the nonlinearity results in a compact wave with a sharp front separating the perturbed region from vacuum. In 