R. Hurtado-Gutiérrez, P.I. Hurtado, C. Pérez-Espigares
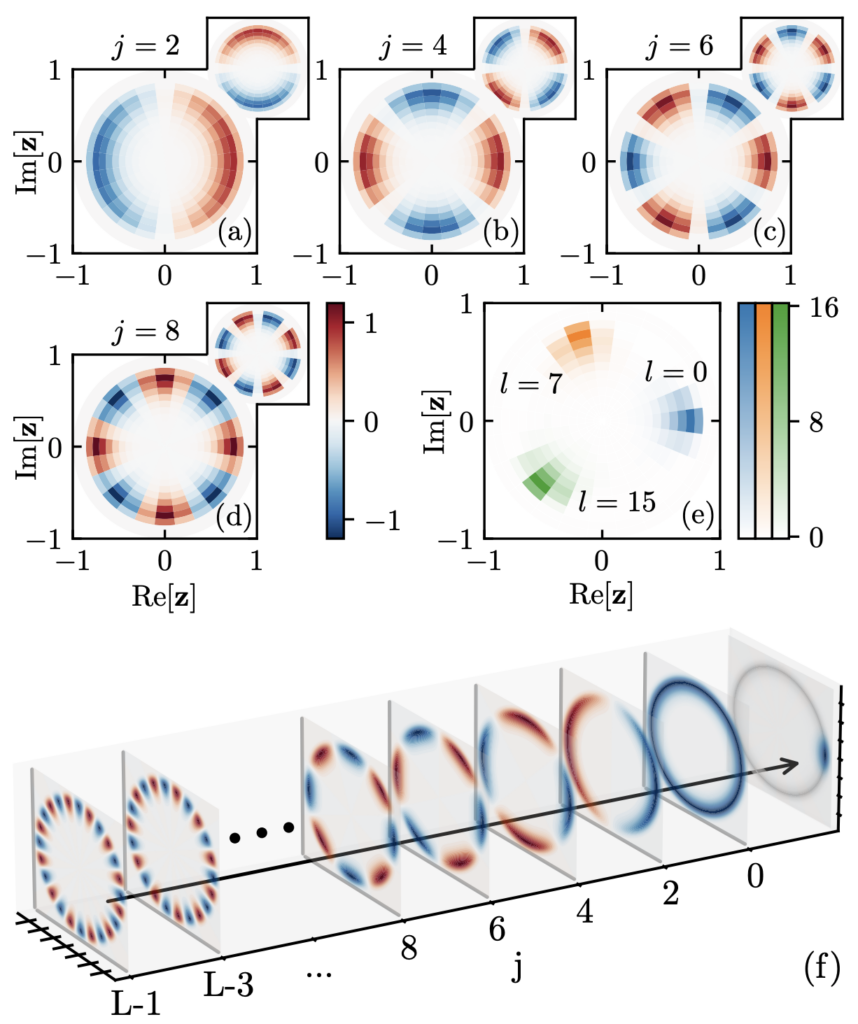
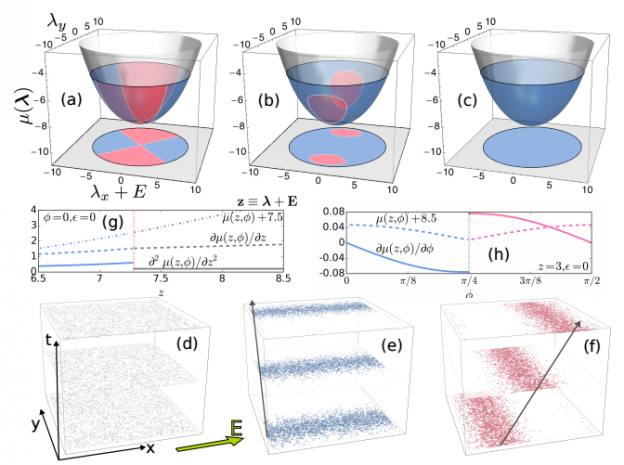
Large deviation theory provides the framework to study the probability of rare fluctuations of time-averaged observables, opening new avenues of research in nonequilibrium physics. One of the most appealing results within this context are dynamical phase transitions (DPTs), which might occur at the level of trajectories in order to maximize the probability of sustaining a rare event. While the Macroscopic Fluctuation Theory has underpinned much recent progress on the understanding of symmetry-breaking DPTs in driven diffusive systems, their microscopic characterization is still challenging. In this work we shed light on the general spectral mechanism giving rise to continuous DPTs not only for driven diffusive systems, but for any jump process in which a discrete ℤn symmetry is broken. By means of a symmetry-aided spectral analysis of the Doob-transformed dynamics, we provide the conditions whereby symmetry-breaking DPTs might emerge and how the different dynamical phases arise from the specific structure of the degenerate eigenvectors. We show explicitly how all symmetry-breaking features are encoded in the subleading eigenvectors of the degenerate manifold. Moreover, by partitioning configuration space into equivalence classes according to a proper order parameter, we achieve a substantial dimensional reduction which allows for the quantitative characterization of the spectral fingerprints of DPTs. We illustrate our predictions in three paradigmatic many-body systems: (i) the 1D boundary-driven weakly asymmetric exclusion process (WASEP), which exhibits a particle-hole symmetry-breaking DPT for current fluctuations, (ii) the 3 and 4-state Potts model, which displays discrete rotational symmetry-breaking DPT for energy fluctuations, and (iii) the closed WASEP which presents a continuous symmetry-breaking DPT to a time-crystal phase characterized by a rotating condensate.
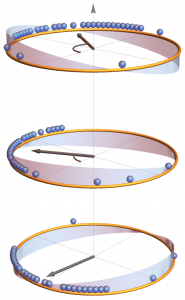
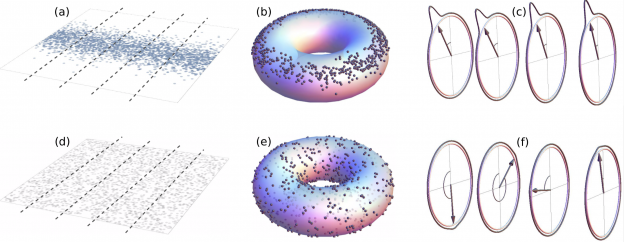
The special issue of European Physical Journal Special Topics has been finally published. It originated at the 14th Granada Seminar on Quantum Systems in and out of equilibrium: Fundamentals, dynamics and applications, which took place in 2017, from June 20 to June 23 in Granada, Spain. This edition was sponsored by the University of Granada through the Department of Electromagnetism and Physics of the Matter and the Faculty of Sciences, the Spanish Minister of Economy, Industry and Competitiveness, and the European Physical Society. There were in this edition a total of 57 lectures and 27 poster contributions covering quantum aspects of thermalization, quantum transport, quantum effects in condensed matter, biology, quantum computation, open quantum systems, quantum fluctuations and large deviations, and quantum thermodynamics.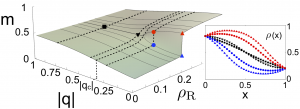
Driven diffusive systems may undergo phase transitions to sustain atypical values of the current. This leads in some cases to symmetry-broken space-time trajectories which enhance the probability of such fluctuations. Here we shed light on both the macroscopic large deviation properties and the microscopic origin of such spontaneous symmetry breaking in the weakly asymmetric exclusion process. By studying the joint fluctuations of the current and a collective order parameter, we uncover the full dynamical phase diagram for arbitrary boundary driving, which is reminiscent of a ℤ2 symmetry-breaking transition. The associated joint large deviation function becomes non-convex below the critical point, where a Maxwell-like violation of the additivity principle is observed. At the microscopic level, the dynamical phase transition is linked to an emerging degeneracy of the ground state of the microscopic generator, from which the optimal trajectories in the symmetry-broken phase follow. In addition, we observe this new symmetry-breaking phenomenon in extensive rare-event simulations of the microscopic dynamics.
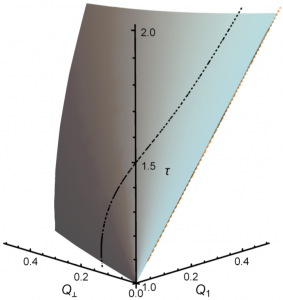
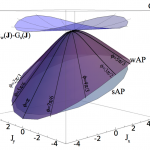The additivity principle (AP) allows to compute the current distribution in many one-dimensional (1d) nonequilibrium systems. Here we extend this conjecture to general d-dimensional driven diffusive systems, and validate its predictions against both numerical simulations of rare events and microscopic exact calculations of three paradigmatic models of diffusive transport in d=2. Crucially, the existence of a structured current vector field at the fluctuating level, coupled to the local mobility, turns out to be essential to understand current statistics in d>1. We prove that, when compared to the straightforward extension of the AP to high-d, the so-called weak AP always yields a better minimizer of the macroscopic fluctuation theory action for current statistics.
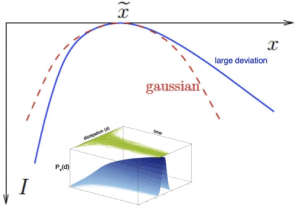Understanding the physics of non-equilibrium systems remains as one of the major open questions in statistical physics. This problem can be partially handled by investigating macroscopic fluctuations of key magnitudes that characterise the non-equilibrium behaviour of the system of interest; their statistics, associated structures and microscopic origin. During the last years, some new general and powerful methods have appeared to delve into fluctuating behaviour that have drastically changed the way to address this problem in the realm of diffusive systems: macroscopic fluctuation theory (MFT) and a set of advanced computational techniques that make it possible to measure the probability of rare events. Notwithstanding, a satisfactory theory is still lacking in a particular case of intrinsically non-equilibrium systems, namely those in which energy is not conserved but dissipated continuously in the bulk of the system (e.g. granular media). In this work, we put forward the dissipated energy as a relevant quantity in this case and analyse in a pedagogical way its fluctuations, by making use of a suitable generalisation of macroscopic fluctuation theory to driven dissipative media.