P.L. Garrido, P.I. Hurtado, D. Manzano, F. de los Santos
The special issue of European Physical Journal Special Topics has been finally published. It originated at the 14th Granada Seminar on Quantum Systems in and out of equilibrium: Fundamentals, dynamics and applications, which took place in 2017, from June 20 to June 23 in Granada, Spain. This edition was sponsored by the University of Granada through the Department of Electromagnetism and Physics of the Matter and the Faculty of Sciences, the Spanish Minister of Economy, Industry and Competitiveness, and the European Physical Society. There were in this edition a total of 57 lectures and 27 poster contributions covering quantum aspects of thermalization, quantum transport, quantum effects in condensed matter, biology, quantum computation, open quantum systems, quantum fluctuations and large deviations, and quantum thermodynamics.
We consider fluctuations of the dissipated energy in nonlinear driven diffusive systems subject to bulk dissipation and boundary driving. With this aim, we extend the recently-introduced macroscopic fluctuation theory to nonlinear driven dissipative media, starting from the fluctuating hydrodynamic equations describing the system mesoscopic evolution. Interestingly, the action associated to a path in mesoscopic phase-space, from which large-deviation functions for macroscopic observables can be derived, has the same simple form as in non-dissipative systems. This is a consequence of the quasi-elasticity of microscopic dynamics, required in order to have a nontrivial competition between diffusion and dissipation at the mesoscale. Euler-Lagrange equations for the optimal density and current fields that sustain an arbitrary dissipation fluctuation are also derived. A perturbative solution thereof shows that the probability distribution of small fluctuations is always gaussian, as expected from the central limit theorem. On the other hand, strong separation from the gaussian behavior is observed for large fluctuations, with a distribution which shows no negative branch, thus violating the Gallavotti-Cohen fluctuation theorem as expected from the irreversibility of the dynamics. The dissipation large-deviation function exhibits simple and general scaling forms for weakly and strongly dissipative systems, with large fluctuations favored in the former case but heavily supressed in the latter. We apply our results to a general class of diffusive lattice models for which dissipation, nonlinear diffusion and driving are the key ingredients. The theoretical predictions are compared to extensive numerical simulations of the microscopic models, and excellent agreement is found. Interestingly, the large-deviation function is in some cases non-convex beyond some dissipation. These results show that a suitable generalization of macroscopic fluctuation theory is capable of describing in detail the fluctuating behavior of nonlinear driven dissipative media.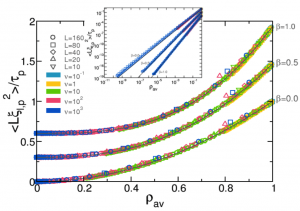
We consider a general class of nonlinear diffusive models with bulk dissipation and boundary driving, and derive its hydrodynamic description in the large size limit. Both the average macroscopic behavior and the fluctuating properties of the hydrodynamic fields are obtained from the microscopic dynamics. This analysis yields a fluctuating balance equation for the local energy density at the mesoscopic level, characterized by two terms: (i) a diffusive term, with a current that fluctuates around its average behavior given by nonlinear Fourier’s law, and (ii) a dissipation term which is a general function of the local energy density. The quasi-elasticity of microscopic dynamics, required in order to have a nontrivial competition between diffusion and dissipation in the macroscopic limit, implies a noiseless dissipation term in the balance equation, so dissipation fluctuations are enslaved to those of the density field. The microscopic complexity is thus condensed in just three transport coefficients, the diffusivity, the mobility and a new dissipation coefficient, which are explicitly calculated within a local equilibrium approximation. Interestingly, the diffusivity and mobility coefficients obey an Einstein relation despite the fully nonequilibrium character of the problem. The general theory here presented is applied to a particular albeit broad family of systems, the simplest nonlinear dissipative variant of the so-called KMP model for heat transport. The theoretical predictions are compared to extensive numerical simulations, and an excellent agreement is found.