Pablo I. Hurtado, Pedro L. Garrido
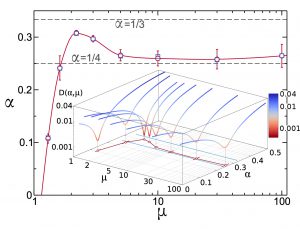Since the discovery of long-time tails, it has been clear that Fourier’s law in low dimensions is typically anomalous, with a size-dependent heat conductivity, though the nature of the anomaly remains puzzling. The conventional wisdom, supported by recent results from nonlinear fluctuating hydrodynamics, is that the anomaly is universal in 1d momentum-conserving systems and belongs in the Kardar-Parisi-Zhang universality class. Here we challenge this picture by using a novel scaling method to show unambiguously that universality breaks down in the paradigmatic 1d diatomic hard-point fluid. Hydrodynamic profiles for a broad set of gradients, densities and sizes all collapse onto an universal master curve, showing that (anomalous) Fourier’s law holds even deep into the nonlinear regime. This allows to solve the macroscopic transport problem for this model, a solution which compares flawlessly with data and, interestingly, implies the existence of a bound on the heat current in terms of pressure. These results question the use of standard fluctuating hydrodynamics to understand anomalous Fourier’s law in 1d, offering a new perspective on transport and its anomalies in low dimensions.