P. I. Hurtado, P.L. Garrido
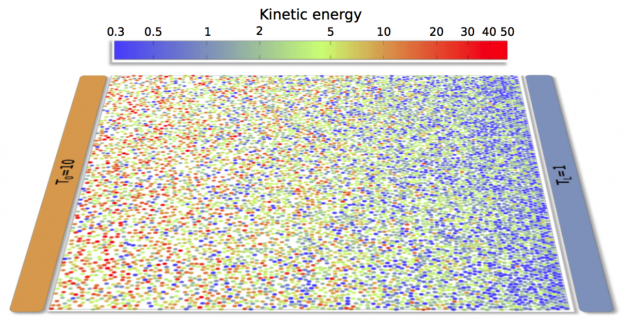
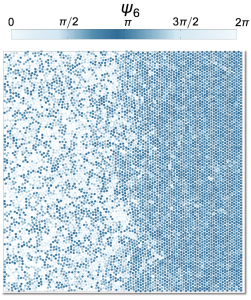 Hard particle systems are among the most successful, inspiring and prolific models of physics. They contain the essential ingredients to understand a large class of complex phenomena, from phase transitions to glassy dynamics, jamming, or the physics of liquid crystals and granular materials, to mention just a few. As we discuss in this paper, their study also provides crucial insights on the problem of transport out of equilibrium. A main tool in this endeavour are computer simulations of hard particles. Here we review some of our work in this direction, focusing on the hard disks fluid as a model system. In this quest we will address, using extensive numerical simulations, some of the key open problems in the physics of transport, ranging from local equilibrium and Fourier’s law to the transition to convective flow in the presence of gravity, the efficiency of boundary dissipation, or the universality of anomalous transport in low dimensions. In particular, we probe numerically the macroscopic local equilibrium hypothesis, which allows to measure the fluid’s equation of state in nonequilibrium simulations, uncovering along the way subtle nonlocal corrections to local equilibrium and a remarkable bulk-boundary decoupling phenomenon in fluids out of equilibrium. We further show that the the hydrodynamic profiles that a system develops when driven out of equilibrium by an arbitrary temperature gradient obey universal scaling laws, a result that allows the determination of transport coefficients with unprecedented precision and proves that Fourier’s law remains valid in highly nonlinear regimes. Switching on a gravity field against the temperature gradient, we investigate numerically the transition to convective flow. We uncover a surprising two-step transition scenario with two different critical thresholds for the hot bath temperature, a first one where convection kicks but gravity hinders heat transport, and a second critical temperature where a percolation transition of streamlines connecting the hot and cold baths triggers efficient convective heat transport. We also address numerically the efficiency of boundary heat baths to dissipate the energy provided by a bulk driving mechanism. As a bonus track, we depart from the hard disks model to study anomalous transport in a related hard-particle system, the $1d$ diatomic hard-point gas. We show unambiguously that the universality conjectured for anomalous transport in $1d$ breaks down for this model, calling into question recent theoretical predictions and offering a new perspective on anomalous transport in low dimensions. Our results show how carefully-crafted numerical simulations of simple hard particle systems can lead to unexpected discoveries in the physics of transport, paving the way to further advances in nonequilibrium physics.
Hard particle systems are among the most successful, inspiring and prolific models of physics. They contain the essential ingredients to understand a large class of complex phenomena, from phase transitions to glassy dynamics, jamming, or the physics of liquid crystals and granular materials, to mention just a few. As we discuss in this paper, their study also provides crucial insights on the problem of transport out of equilibrium. A main tool in this endeavour are computer simulations of hard particles. Here we review some of our work in this direction, focusing on the hard disks fluid as a model system. In this quest we will address, using extensive numerical simulations, some of the key open problems in the physics of transport, ranging from local equilibrium and Fourier’s law to the transition to convective flow in the presence of gravity, the efficiency of boundary dissipation, or the universality of anomalous transport in low dimensions. In particular, we probe numerically the macroscopic local equilibrium hypothesis, which allows to measure the fluid’s equation of state in nonequilibrium simulations, uncovering along the way subtle nonlocal corrections to local equilibrium and a remarkable bulk-boundary decoupling phenomenon in fluids out of equilibrium. We further show that the the hydrodynamic profiles that a system develops when driven out of equilibrium by an arbitrary temperature gradient obey universal scaling laws, a result that allows the determination of transport coefficients with unprecedented precision and proves that Fourier’s law remains valid in highly nonlinear regimes. Switching on a gravity field against the temperature gradient, we investigate numerically the transition to convective flow. We uncover a surprising two-step transition scenario with two different critical thresholds for the hot bath temperature, a first one where convection kicks but gravity hinders heat transport, and a second critical temperature where a percolation transition of streamlines connecting the hot and cold baths triggers efficient convective heat transport. We also address numerically the efficiency of boundary heat baths to dissipate the energy provided by a bulk driving mechanism. As a bonus track, we depart from the hard disks model to study anomalous transport in a related hard-particle system, the $1d$ diatomic hard-point gas. We show unambiguously that the universality conjectured for anomalous transport in $1d$ breaks down for this model, calling into question recent theoretical predictions and offering a new perspective on anomalous transport in low dimensions. Our results show how carefully-crafted numerical simulations of simple hard particle systems can lead to unexpected discoveries in the physics of transport, paving the way to further advances in nonequilibrium physics.
J. Stat. Phys. 180, 474 (2020)



 The special issue of European Physical Journal Special Topics has been finally published. It originated at the 14th Granada Seminar on Quantum Systems in and out of equilibrium: Fundamentals, dynamics and applications, which took place in 2017, from June 20 to June 23 in Granada, Spain. This edition was sponsored by the University of Granada through the Department of Electromagnetism and Physics of the Matter and the Faculty of Sciences, the Spanish Minister of Economy, Industry and Competitiveness, and the European Physical Society. There were in this edition a total of 57 lectures and 27 poster contributions covering quantum aspects of thermalization, quantum transport, quantum effects in condensed matter, biology, quantum computation, open quantum systems, quantum fluctuations and large deviations, and quantum thermodynamics.
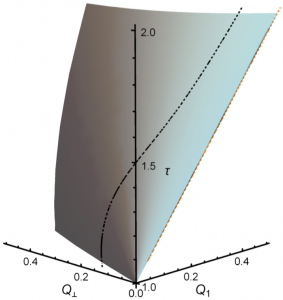
The special issue of European Physical Journal Special Topics has been finally published. It originated at the 14th Granada Seminar on Quantum Systems in and out of equilibrium: Fundamentals, dynamics and applications, which took place in 2017, from June 20 to June 23 in Granada, Spain. This edition was sponsored by the University of Granada through the Department of Electromagnetism and Physics of the Matter and the Faculty of Sciences, the Spanish Minister of Economy, Industry and Competitiveness, and the European Physical Society. There were in this edition a total of 57 lectures and 27 poster contributions covering quantum aspects of thermalization, quantum transport, quantum effects in condensed matter, biology, quantum computation, open quantum systems, quantum fluctuations and large deviations, and quantum thermodynamics.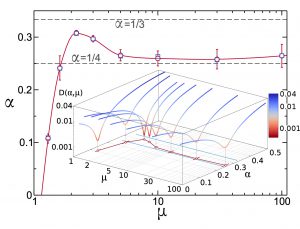 Since the discovery of long-time tails, it has been clear that Fourier’s law in low dimensions is typically anomalous, with a size-dependent heat conductivity, though the nature of the anomaly remains puzzling. The conventional wisdom, supported by recent results from nonlinear fluctuating hydrodynamics, is that the anomaly is universal in 1d momentum-conserving systems and belongs in the Kardar-Parisi-Zhang universality class. Here we challenge this picture by using a novel scaling method to show unambiguously that universality breaks down in the paradigmatic 1d diatomic hard-point fluid. Hydrodynamic profiles for a broad set of gradients, densities and sizes all collapse onto an universal master curve, showing that (anomalous) Fourier’s law holds even deep into the nonlinear regime. This allows to solve the macroscopic transport problem for this model, a solution which compares flawlessly with data and, interestingly, implies the existence of a bound on the heat current in terms of pressure. These results question the use of standard fluctuating hydrodynamics to understand anomalous Fourier’s law in 1d, offering a new perspective on transport and its anomalies in low dimensions.
Since the discovery of long-time tails, it has been clear that Fourier’s law in low dimensions is typically anomalous, with a size-dependent heat conductivity, though the nature of the anomaly remains puzzling. The conventional wisdom, supported by recent results from nonlinear fluctuating hydrodynamics, is that the anomaly is universal in 1d momentum-conserving systems and belongs in the Kardar-Parisi-Zhang universality class. Here we challenge this picture by using a novel scaling method to show unambiguously that universality breaks down in the paradigmatic 1d diatomic hard-point fluid. Hydrodynamic profiles for a broad set of gradients, densities and sizes all collapse onto an universal master curve, showing that (anomalous) Fourier’s law holds even deep into the nonlinear regime. This allows to solve the macroscopic transport problem for this model, a solution which compares flawlessly with data and, interestingly, implies the existence of a bound on the heat current in terms of pressure. These results question the use of standard fluctuating hydrodynamics to understand anomalous Fourier’s law in 1d, offering a new perspective on transport and its anomalies in low dimensions.