C. Gutiérrez-Ariza, P. I. Hurtado
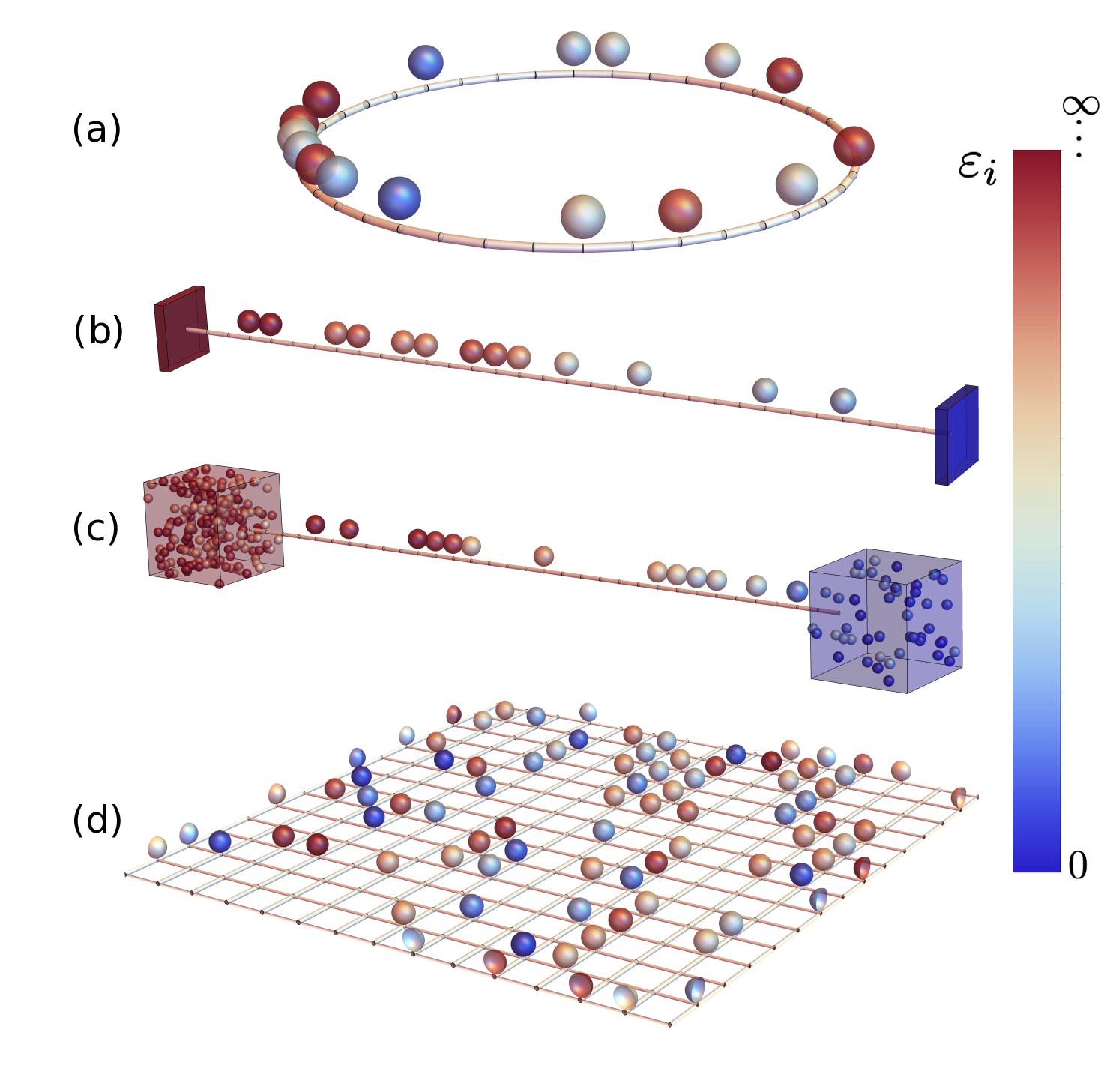We introduce a general class of stochastic lattice gas models, and derive their fluctuating hydrodynamics description in the large size limit under a local equilibrium hypothesis. The model consists in energetic particles on a lattice subject to exclusion interactions, which move and collide stochastically with energy-dependent rates. The resulting fluctuating hydrodynamics equations exhibit nonlinear coupled particle and energy transport, including particle currents due to temperature gradients (Soret effect) and energy flow due to concentration gradients (Dufour effect). The microscopic dynamical complexity is condensed in just two matrices of transport coefficients: the diffusivity matrix (or equivalently the Onsager matrix) generalizing Fick-Fourier’s law, and the mobility matrix controlling current fluctuations, which are coupled via a fluctuation-dissipation theorem. Interestingly, the positivity of entropy production in the system then leads to detailed constraints on the microscopic dynamics. We further demonstrate the Gaussian character of the noise terms affecting the local currents. The so-called kinetic exclusion process has as limiting cases two of the most paradigmatic models of nonequilibrium physics, namely the symmetric simple exclusion process of particle diffusion and the Kipnis-Marchioro-Presutti model of heat flow, making it the ideal testbed where to further develop modern theories of nonequilibrium behavior.
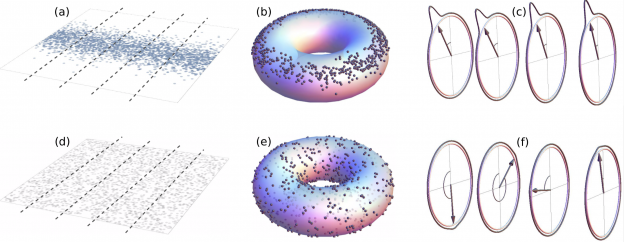
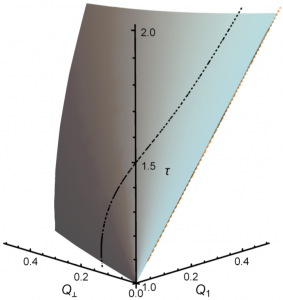
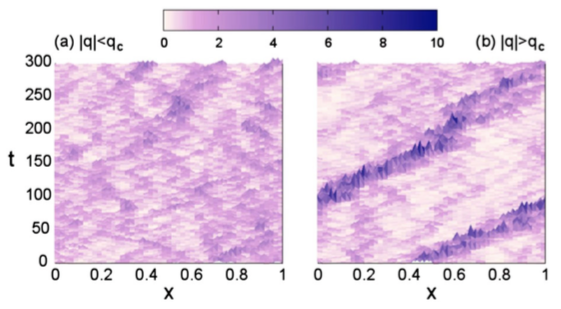
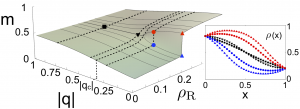
Driven diffusive systems may undergo phase transitions to sustain atypical values of the current. This leads in some cases to symmetry-broken space-time trajectories which enhance the probability of such fluctuations. Here we shed light on both the macroscopic large deviation properties and the microscopic origin of such spontaneous symmetry breaking in the weakly asymmetric exclusion process. By studying the joint fluctuations of the current and a collective order parameter, we uncover the full dynamical phase diagram for arbitrary boundary driving, which is reminiscent of a ℤ2 symmetry-breaking transition. The associated joint large deviation function becomes non-convex below the critical point, where a Maxwell-like violation of the additivity principle is observed. At the microscopic level, the dynamical phase transition is linked to an emerging degeneracy of the ground state of the microscopic generator, from which the optimal trajectories in the symmetry-broken phase follow. In addition, we observe this new symmetry-breaking phenomenon in extensive rare-event simulations of the microscopic dynamics.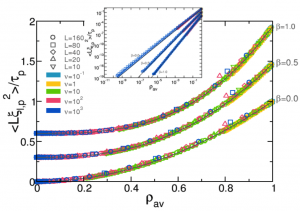
We consider a general class of nonlinear diffusive models with bulk dissipation and boundary driving, and derive its hydrodynamic description in the large size limit. Both the average macroscopic behavior and the fluctuating properties of the hydrodynamic fields are obtained from the microscopic dynamics. This analysis yields a fluctuating balance equation for the local energy density at the mesoscopic level, characterized by two terms: (i) a diffusive term, with a current that fluctuates around its average behavior given by nonlinear Fourier’s law, and (ii) a dissipation term which is a general function of the local energy density. The quasi-elasticity of microscopic dynamics, required in order to have a nontrivial competition between diffusion and dissipation in the macroscopic limit, implies a noiseless dissipation term in the balance equation, so dissipation fluctuations are enslaved to those of the density field. The microscopic complexity is thus condensed in just three transport coefficients, the diffusivity, the mobility and a new dissipation coefficient, which are explicitly calculated within a local equilibrium approximation. Interestingly, the diffusivity and mobility coefficients obey an Einstein relation despite the fully nonequilibrium character of the problem. The general theory here presented is applied to a particular albeit broad family of systems, the simplest nonlinear dissipative variant of the so-called KMP model for heat transport. The theoretical predictions are compared to extensive numerical simulations, and an excellent agreement is found.
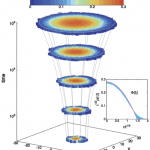We analyze the spread of a localized peak of energy into vacuum for nonlinear diffusive processes. In contrast with standard diffusion, the nonlinearity results in a compact wave with a sharp front separating the perturbed region from vacuum. In 