Author Archives: phurtado

Quantum systems in and out of equilibrium: Fundamentals, dynamics and applications

P.L. Garrido, P.I. Hurtado, D. Manzano, F. de los Santos

The special issue of European Physical Journal Special Topics has been finally published. It originated at the 14th Granada Seminar on Quantum Systems in and out of equilibrium: Fundamentals, dynamics and applications, which took place in 2017, from June 20 to June 23 in Granada, Spain. This edition was sponsored by the University of Granada through the Department of Electromagnetism and Physics of the Matter and the Faculty of Sciences, the Spanish Minister of Economy, Industry and Competitiveness, and the European Physical Society. There were in this edition a total of 57 lectures and 27 poster contributions covering quantum aspects of thermalization, quantum transport, quantum effects in condensed matter, biology, quantum computation, open quantum systems, quantum fluctuations and large deviations, and quantum thermodynamics.

Eur. Phys. J Special Topics 227, 201 (2018)

Dynamical criticality in driven systems: non-perturbative physics, microscopic origin and direct observation

C. Pérez-Espigares, F. Carollo, J.P. Garrahan, P.I. Hurtado

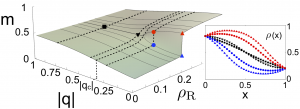Driven diffusive systems may undergo phase transitions to sustain atypical values of the current. This leads in some cases to symmetry-broken space-time trajectories which enhance the probability of such fluctuations. Here we shed light on both the macroscopic large deviation properties and the microscopic origin of such spontaneous symmetry breaking in the weakly asymmetric exclusion process. By studying the joint fluctuations of the current and a collective order parameter, we uncover the full dynamical phase diagram for arbitrary boundary driving, which is reminiscent of a ℤ2 symmetry-breaking transition. The associated joint large deviation function becomes non-convex below the critical point, where a Maxwell-like violation of the additivity principle is observed. At the microscopic level, the dynamical phase transition is linked to an emerging degeneracy of the ground state of the microscopic generator, from which the optimal trajectories in the symmetry-broken phase follow. In addition, we observe this new symmetry-breaking phenomenon in extensive rare-event simulations of the microscopic dynamics.

Phys. Rev. E 98, 060102(R) (2018); arXiv:1807.10235

Harnessing symmetry to control quantum transport

D. Manzano and P.I. Hurtado

Controlling transport in quantum systems holds the key to many promising quantum technologies. Here we review the power of symmetry as a resource to manipulate quantum transport, and apply these ideas to engineer novel quantum devices. Using tools from open quantum systems and large deviation theory, we show that symmetry-mediated control of transport is enabled by a pair of twin dynamic phase transitions in current statistics, accompanied by a coexistence of different transport channels. By playing with the symmetry decomposition of the initial state, one can modulate the importance of the different transport channels and hence control the flowing current. Motivated by the problem of energy harvesting we illustrate these ideas in open quantum networks, an analysis which leads to the design of a symmetry-controlled quantum thermal switch. We review an experimental setup recently proposed for symmetry-mediated quantum control in the lab based on a linear array of atom-doped optical cavities, and the possibility of using transport as a probe to uncover hidden symmetries, as recently demonstrated in molecular junctions, is also discussed. Overall, these results demonstrate the importance of symmetry not only as a organizing principle in physics but also as a tool to control quantum systems.

Adv. in Phys. 67, 1 (2018); arXiv:1707.07895