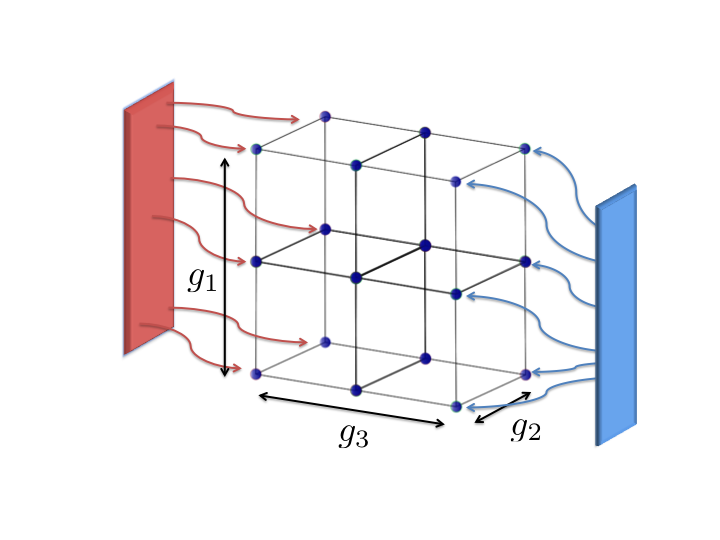
Quantum transport in lattices is a major field of study nowadays. It has been probed that a lattice composed by harmonic oscillators connected to two thermal baths at different temperatures behaves ballistically in any dimension [1]. On the other hand, if the lattice is composed by spins it is ballistic only in the one-dimensional case [2, 3]. In the simplest two-dimensional spin lattice, a ladder, it has been numerically probed the existence of both ballistic and non-ballistic channels [4].
In this talk, I will show that both fermionic and bosonic uniform d-dimensional lattices can be reduced to a set of independent one-dimensional chains [5]. This reduction leads to the expression for ballistic energy fluxes in uniform fermionic and bosonic lattices. By the use of the Jordan-Wigner transformation, we can extend our analysis to spin lattices, proving the coexistence of both ballistic and non-ballistic subspaces in any dimension and for any system size. We then relate the nature of transport to the number of excitations in the homogeneous spin lattice, indicating that a single excitation always propagates ballistically and that the non-ballistic behaviour of uniform spin lattices is a consequence of the interaction between different excitations.
References:
[1] A. Asadian, D. Manzano, M. Tiersch, and H.J. Briegel. Phys. Rev. E 87, 012109 (2013)
[2] M. Znidaric. Phys. Rev. E 83, 011108 (2011).
[3] D. Manzano, M. Tiersch, A. Asadian, and H.J. Briegel. Phys. Rev. E 86, 061118 (2012).
[4] M. Znidaric. Phys. Rev. Lett. 110, 070602 (2013).
[5] D. Manzano, C. Chuang, and J. Cao. New J. Phys. 18, 043044 (2016).
Conferenciante: Daniel Manzano, Departamento de Electromagnetismo y Física de la Materia. Universidad de Granada
Fecha y hora: Viernes 22 de febrero a las 12:00
Lugar: Aula de informática. Departamento de Física de la Materia. Planta baja del edificio de Física. Facultad de Ciencias
